h  Stunden   Hours
  m  Minuten   Minutes
  s  Sekunden  Seconds
  °  Grad      Degrees
  '  Bogenminuten oder Winkelminuten    Minutes of arc
  "  Bogensekunden oder Winkelsekunden  Seconds of arc

 24h = 1440m = 86400s =    360° = 21600' = 1296000"
  1h =   60m =  3600s =     15° =   900' =   54000"
          4m =   240s =      1° =    60' =    3600"
          1m =    60s =    1/4° =    15' =     900" 
                   4s =   1/60° =     1' =      60"
                   1s =  1/240° =   1/4' =      15"
               1/15s = 1/3600° =  1/60' =       1"

Radius des Beugungsscheibchens:

b = 1.22 lambda f / D

oder

b = 1.22 lambda N

mit lambda = Wellenlänge des Lichts, z.B. 550nm
    f = Brennweite
    D = Objektiv-Durchmesser
    N = Öffnungsverhältnis

Beispiele für lambda = 550nm:
N =  1  -->  b =  0.67µm
N =  2  -->  b =  1.34µm
N =  3  -->  b =  2.0µm
N =  4  -->  b =  2.7µm
N =  5  -->  b =  3.4µm
N =  6  -->  b =  4.0µm
N =  8  -->  b =  5.4µm
N = 10  -->  b =  6.7µm
N = 12  -->  b =  8.1µm
N = 15  -->  b = 10.1µm
N = 20  -->  b = 13.4µm
N = 25  -->  b = 16.8µm
N = 30  -->  b = 20.1µm

Beispiele für lambda = 632.8nm:
N =  1  -->  b =  0.77µm
N =  2  -->  b =  1.54µm
N =  3  -->  b =  2.3µm
N =  4  -->  b =  3.1µm
N =  5  -->  b =  3.9µm
N =  6  -->  b =  4.6µm
N =  8  -->  b =  6.2µm
N = 10  -->  b =  7.7µm
N = 12  -->  b =  9.3µm
N = 15  -->  b = 11.6µm
N = 20  -->  b = 15.4µm
N = 25  -->  b = 19.3µm
N = 30  -->  b = 23.2µm
 

Auflösungsvermögen (Winkel-Radius des Beugungsscheibchens):

a = 1.22 lambda / D     (Einheit: Radiant)
a = 69.9 lambda / D     (Einheit: Grad)
a = 4194 lambda / D     (Einheit: Bogenminuten)
a = 251643 lambda / D   (Einheit: Bogensekuden)

mit lambda = Wellenlänge des Lichts, z.B. 550nm
         D = Objektiv-Durchmesser

Beispiele für lambda = 550nm:
D = 0.001mm  -->  a = 38.4°
D =  0.01mm  -->  a =  3.8°
D =   0.1mm  -->  a =   23'
D =     1mm  -->  a =  138"
D =     5mm  -->  a = 27.7"
D =    10mm  -->  a = 13.8"
D =    20mm  -->  a =  6.9"
D =    50mm  -->  a =  2.8"
D =    75mm  -->  a =  1.8"
D =   100mm  -->  a =  1.4"
D =   150mm  -->  a =  0.92" 
D =   200mm  -->  a =  0.69"
D =   300mm  -->  a =  0.46"
D =   400mm  -->  a =  0.35"
D =   500mm  -->  a =  0.28"
D =   750mm  -->  a =  0.18"
D =  1000mm  -->  a =  0.14"
D =  1250mm  -->  a =  0.11"
 

Eine Barlowlinse verlängert die Brennweite eines Teleskops um den Faktor V, eine Shapley-Linse verkürzt die Brennweite.
Die Barlowlinse ist konkav: )(
Die Shapleylinse ist konvex: ()
************************************************
Eselsbrücke:
Ist der Bauch konvav, war das Mädchen brav.
Ist der Bauch konvex, hatte das Mädchen Sex.
************************************************
Der Vergrösserungsfaktor V wird so berechnet:
A Barlow lens increases the focal length of a telescope by a factor V, a Shapley lens decreases the focal length.
The Barlow lens is concave: )(
The Shapley lens is convex: ()
The factor V is calculated by this formula: 

V = 1 - (e / f) 

e ist der Abstand von der Barlow-(oder Shapley-) Linse zum neuen Fokus.
e is the distance from the Barlow (or Shapley) lens to the new focus.
f ist die Brennweite der Barlow-(oder Shapley-) Linse.  f is the focal length of the Barlow (or Shapley) lens
Bei Barlow-Linsen ist V > 1 und f < 0    For a Barlow lens: V > 1 and f < 0
Bei Shapley-Linsen ist V < 1 und f > 0    For a Shapley lens: V < 1 and f > 0

Der ursprüngliche Fokus (ohne Linse) wird bei Verwendung einer Barlowlinse um x nach hinten verschoben.
The old focus (without lens) will be shifted towards the eyepiece by distance x if a Barlow lens is used.

x = e (1 - (1 / V)) 

Bei Verwendung einer Shapley-Linse ist x negativ, der Brennpunkt wird also nach vorne verschoben.
When using a Shapley lens x is negative, so that the focus is shifted towards the objective.

Die gleichen Formeln nach anderen Variablen aufgelöst:
The same formulas solved for other variables:

e = f (1 - V)

e = (x V) / (V - 1)

e = x / 2 +- sqrt(x^2 / 4 - (x f))

f = e / (1 - V)

f = x / (2 - V - (1 / V))

V = e / (e - x)

x = f (2 - V - (1 / V))

x = e (1 - f / (f - e))

x = e^2 / (e - f)

e - x = e (f / (f - e))

e - x = e / V

e - x = x / (V - 1)

e - x = -x / 2 +- sqrt(x^2 / 4 - (x f))
 

Der Vergrösserungsfaktor lässt sich nicht beliebig steigern, weil irgendwann der Durchmesser der Barlowlinse zu klein wird. Der Linsen-Durchmesser d muss (für 0mm Bildfeld-Durchmesser) mindestens so gross sein:
There is an upper limit for the factor V because at some point the diameter of the Barlow lens becomes too small. The minimum lens diameter d (for zero field diameter) is:

d = (e - x) / N 

wobei mit N das Öffnungsverhältnis des Teleskops gemeint ist, also (Brennweite / Objektivdurchmesser).
where N is the focal ratio of the telescope (focal length / objective diameter).
 

Wenn der Durchmesser der Barlow-Linse kleiner ist als die Formel angibt, dann ist zwar der Vergrösserungsfaktor so wie berechnet, aber es wird nicht die volle Öffnung des Teleskops verwendet.
If the diameter of the Barlow lens is smaller than given by the above formula, then the factor V is still as calculated, but you aren't using the full aperture of the telescope.

Praktisch möchte man natürlich mehr als 0mm Bildfeld-Durchmesser haben, also muss die Linse entsprechend grösser sein:
In practice you want more than zero field diameter, so that the lens diameter must be bigger:

d = (e - x) / N + Bf1    (Dies ist eine Näherungsformel für Linsen, die nahe an der Bildebene liegen)
                         (This is an approximation for lenses which are near the focal plane)

wobei Bf1 der Bildfeld-Durchmesser im ursprünglichen Fokus (d.h. ohne Linse) ist.
where Bf1 is the field diameter in the original focal plane (without lens).

Mit Barlow-Linse wird das Bildfeld größer, bzw. mit Shapley-Linse wird es kleiner:
With a Barlow lens the field diameter increases, with a Shapley lens it decreases:

Bf2 = Bf1 * V

wobei Bf2 der Bildfeld-Durchnesser ist, der sich mit Barlow- oder Shapley-Linse ergibt.
where Bf2 is the resulting field diameter with Barlow or Shapley lens.

d = (e - x) / N + Bf2 / V   (Dies ist eine Näherungsformel für Linsen, die nahe an der Bildebene liegen)
                            (This is an approximation for lenses which are near the focal plane)
oder or

d = (e - x) * (1 / N + Bf2 / e)
 

-- Alle Formeln sind exakte Lösungen, sofern nicht anders vermerkt. 
-- Bitte beim Ausdrucken keine Proportionalschrift verwenden, und darauf achten dass die Seite breit genug ist!
-- Wer Fehler findet möge mir das bitte sagen!
-- All formulas are exact solutions unless otherwise noted.
-- When you print out this page, make sure you use "Courier New" and the page is wide enough.
-- If you find bugs, please let me know!
 

Der sphärische Spiegel  The spherical mirror

Oberflächenform: Surface profile:

  y = R - sqrt(R^2 - x^2)

  mit R = Krümmungsradius der Sphäre  Sphere's radius of curvature
      x = Koordinate in radialer Richtung  coordinate in radial direction
 

Erste Ableitung:  First differential:

  y' = x / sqrt(R^2 - x^2)
 

Zweite Ableitung:  Second differential:

  y'' = (R^2 - x^2)^(-1/2) + x^2 (R^2 - x^2)^(-3/2) 
 

Pfeilhöhe (Tiefe des Spiegels in der Mitte):  Sagitta in the middle of the mirror:

  p = R - sqrt(R^2 - (D^2)/4) 

  mit R = Krümmungsradius der Sphäre  Sphere's radius of curvature
      D = Durchmesser des Spiegels  Diameter of the mirror
 

Krümmungsradius bei gegebener Pfeilhöhe:  Radius of curvature for known sagitta:

      D^2    p
  R = --- + ---
      8 p    2

 mit  D = Durchmesser des Spiegels  Diameter of the mirror
      p = Pfeilhöhe   Sagitta in the middle of the mirror
 

Beim Schleifen entferntes Volumen, ausgehend von einer Planfläche:
Volume that is removed during grinding, starting from a flat:

  V = Pi p^2 (R - p/3)

  mit Pi = 3.1415...
      p = Pfeilhöhe  Sagitta in the middle of the mirror
      R = Krümmungsradius  Sphere's radius of curvature
 

Oberflächenform in Reihendarstellung:  Surface profile as a series:

      x^2    x^4     x^6      5 x^8     7 x^10    21 x^12
  y = --- + ----- + ------ + ------- + ------- + --------- + ... 
      2 R   8 R^3   16 R^5   128 R^7   256 R^9   1024 R^11

  mit R = Krümmungsradius der Sphäre  Sphere's radius of curvature
      x = Koordinate in radialer Richtung  coordinate in radial direction
 

Erste Ableitung in Reihendarstellung:  First differential as a series:

        x     x^3    3 x^5    5 x^7    35 x^9    63 x^11
  y' = --- + ----- + ----- + ------ + ------- + -------- + ... 
        R    2 R^3   8 R^5   16 R^7   128 R^9   256 R^11
 

Zweite Ableitung in Reihendarstellung:  Second differential as a series:

         1    3 x^2   15 x^4   35 x^6   315 x^8   693 x^10
  y'' = --- + ----- + ------ + ------ + ------- + -------- + ... 
         R    2 R^3    8 R^5   16 R^7   128 R^9   256 R^11 
 
 

Sphärometer zur Messung des Krümmungsradius:
Spherometer for measuring the radius of curvature:

  Fall 1: Der Messwert und der Krümmungsradius werden immer als positiv angenommen:
  Case 1: The measurement value and the radius of curvature are always assumed to be positive:

       a^2     h
  R = ----- + --- +- b
       2 h     2

  wobei das "+" für konkave Oberflächen gilt, und das "-" für konvexe Oberflächen.
  where the "+" sign is used for concave surfaces and the "-" sign is used for cenvex surfaces.

  mit R = unbekannter Radius der Testfläche (immer positiv)  unknown radius of curvature (always positive)
      a = Radius von der Mitte (Mess-Stelle) bis zur Mitte der 3 Auflage-Kugeln 
  distance from the measurement point to the center of 3 balls
      b = Radius der kleinen Auflage-Kugeln  radius of the 3 small balls
      h = Messwert (immer positiv), bezogen auf eine Planfläche
  measurement value (always positive), with respect to flat surface
 

  Fall 2: Für den Messwert und den Krümmungsradius werden beide Vorzeichen zugelassen:
  Case 2: The measurement value and the radius of curvature can be positive or negative:

       a^2     h
  R = ----- + --- - b
       2 h     2

  mit R = unbekannter Radius der Testfläche (positiv = konvex, negativ = konkav)
  unknown radius of curvature (positive = convex, negative = concave)
      a = Radius von der Mitte (Mess-Stelle) bis zur Mitte der 3 Auflage-Kugeln 
  distance from the measurement point to the center of 3 balls
      b = Radius der kleinen Auflage-Kugeln  radius of the 3 small balls
      h = Messwert (positiv = konvex, negativ = konkav, 0 = Planfläche)
  measurement value (positive = convex, negative = concave, 0 = flat)
 

Der parabolische Spiegel   The parabolic mirror

Oberflächenform: Surface profile:

  y = x^2 / (4 f)

  mit f = Brennweite  focal length
      x = Koordinate in radialer Richtung  coordinate in radial direction
 

Erste Ableitung:  First differential:

  y' = x / (2 f)
 

Zweite Ableitung:  Second differential:

  y'' = 1 / (2 f)
 

Pfeiltiefe (Scheiteltiefe, Tiefe des Spiegels in der Mitte):
Sagitta in the middle of the mirror:

  s = D^2 / (16 f)

  mit f = Brennweite  focal length
      D = Durchmesser des Spiegels  diameter of the mirror
 

Beim Schleifen entferntes Volumen, ausgehend von einer Planfläche:
Volume that is removed during grinding, starting from a flat:

  V = Pi D^4 / (128 f)

  mit Pi = 3.1415...
      D = Durchmesser des Spiegels  diameter of the mirror
      f = Brennweite  focal length
 

Volumen eines Parabolspiegels, Rückseite plan:
Volume of a parabolic mirror, back side flat:

    Pi * D^2   (      D^2   )
V = -------- * ( h - ------ )
       4       (     32 * f )

  mit Pi = 3.1415...
      D = Durchmesser des Spiegels  diameter of the mirror
      h = Dicke am Rand  Thickness at the edge of the mirror
      f = Brennweite  focal length
 

Volumen eines Parabolspiegels mit zentraler Bohrung, Rückseite plan:
Volume of a parabolic mirror with central bore, back side flat:

    Pi * (D^2 - d^2)   (     D^2 - d^2 )
V = ---------------- * ( h - --------- )
           4           (      32 * f   )

  mit Pi = 3.1415...
      D = Durchmesser des Spiegels  diameter of the mirror
      d = Durchmesser der zentralen Bohrung  diameter of the central bore mirror
      h = Dicke am Rand  Thickness at the edge of the mirror
      f = Brennweite  focal length

Volumen eines Parabolspiegels, Rückseite konvex oder konkav:
Volume of a parabolic mirror, back side convex or concave:

    Pi * D^2   (      D^2      s  )
V = -------- * ( h - ------ - --- )
       4       (     32 * f    2  )

  mit Pi = 3.1415...
      D = Durchmesser des Spiegels  diameter of the mirror
      h = Dicke am Rand  Thickness at the edge of the mirror
      f = Brennweite  focal length
      s = Pfeiltiefe der Rückseite in der Mitte  sagitta of back side
          Rückseite konvex --> s ist negativ    back side convex --> s is negative
          Rückseite konkav --> s ist positiv    back side concave --> s is positive
 

Schwerpunkt eines Parabolspiegels:
Center of Gravity of Parabolic Mirror:

        D^2 (24 h f - D^2)
  dx = -------------------
       48 f (32 h f - D^2)

  oder  or

        D (24 h N - D)
  dx = -----------------
       48 N (32 h N - D)

  oder  or

       3 h s - 2 s^2
  dx = -------------
        12 h - 6 s

  mit dx = Verschiebung des Schwerpunktes aus der Mitte des Zylinders heraus
  Offset of center of gravity from the center of cylinder
      h = Dicke des Spiegels am Rand   Thickness at the edge of the mirror
      D = Durchmesser des Spiegels  diameter of the mirror
  f = Brennweite   focal length
      N = f / D = Öffnungsverhältnis  focal ratio
      s = Pfeiltiefe   sagitta
      Annahme: Die Rückseite ist plan.  Assuming the back side is flat.
 

  Lage des Schwerpunktes in Prozent der Spiegeldicke:
  Position of center of gravity in percent of the mirror thickness:

       768 N^2 - A^2
  V = --------------- * 100%
      48 N (32 N - A)

  mit V = Lage des Schwerpunktes in Prozent der Spiegeldicke, gemessen von der Vorderkante
          Position of center of gravity in percent of the mirror thickness, measured from the front edge
      A = D / h = Verhältnis Durchmesser / Dicke    diameter / thickness ratio
      N = f / D = Öffnungsverhältnis   focal ratio
 

	N = 2.0	N = 2.5	N = 3.0	N = 3.5	N = 4.0	N = 4.5	N = 5.0	N = 6.0	N = 8.0	N = 10.0
A = 4	53.06%	52.46%	52.05%	51.76%	51.55%	51.38%	51.24%	51.03%	50.78%	50.62%
A = 4.5	53.43%	52.76%	52.31%	51.98%	51.74%	51.55%	51.39%	51.16%	50.87%	50.70%
A = 5	53.80%	53.06%	52.56%	52.20%	51.93%	51.72%	51.55%	51.29%	50.97%	50.78%
A = 5.5	54.16%	53.35%	52.81%	52.41%	52.12%	51.88%	51.70%	51.42%	51.07%	50.85%
A = 6	54.53%	53.65%	53.06%	52.63%	52.31%	52.05%	51.85%	51.55%	51.16%	50.93%
A = 6.5	54.89%	53.94%	53.30%	52.84%	52.49%	52.22%	52.00%	51.67%	51.26%	51.01%
A = 7	55.24%	54.24%	53.55%	53.06%	52.68%	52.39%	52.15%	51.80%	51.35%	51.09%
A = 7.5	55.60%	54.53%	53.80%	53.27%	52.87%	52.56%	52.31%	51.93%	51.45%	51.16%
A = 8	55.95%	54.81%	54.04%	53.50%	53.05%	52.72%	52.46%	52.05%	51.55%	51.24%
A = 9	56.65%	55.39%	54.53%	53.90%	53.43%	53.06%	52.76%	52.31%	51.74%	51.39%
A = 10	57.33%	55.95%	55.01%	54.32%	53.80%	53.39%	53.06%	52.56%	51.93%	51.55%
A = 11	58.00%	56.51%	55.48%	54.73%	54.16%	53.71%	53.35%	52.81%	52.12%	51.70%
A = 12	58.65%	57.06%	55.95%	55.14%	54.53%	54.04%	53.65%	53.06%	52.31%	51.85%
A = 13	59.29%	57.60%	56.42%	55.55%	54.89%	54.36%	53.94%	53.30%	52.49%	52.00%
A = 14	59.92%	58.13%	56.88%	55.95%	55.24%	54.69%	54.24%	53.55%	52.68%	52.15%
A = 15	60.52%	58.65%	57.33%	56.35%	55.60%	55.01%	54.53%	53.80%	52.87%	52.31%
A = 16	61.11%	59.17%	57.78%	56.75%	55.95%	55.32%	54.81%	54.04%	53.06%	52.46%
A = 18	62.23%	60.16%	58.65%	57.52%	56.65%	55.95%	55.39%	54.53%	53.43%	52.76%
A = 20	63.26%	61.11%	59.50%	58.28%	57.33%	56.57%	55.95%	55.01%	53.80%	53.06%

 

Krümmungsradius an einer beliebigen Stelle:
Radius of curvature at any point:

                   x^2
  Rad = 2 f ( 1 + ----- ) ^(3/2)
                 4 f^2

  oder
                      3 x^4    x^6
  Rad = sqrt( 3 x^2 + ----- + ------ + 4 f^2 )
                      4 f^2   16 f^4

  mit f = Brennweite  focal length
     x = Koordinate in radialer Richtung  coordinate in radial direction
 

Koordinaten des Krümmungsmittelpunkts:
(Man beachte: der Krümmungsmittelpunkt liegt nicht genau auf der optischen Achse!)
Coordinates of the center of curvature:
(Please note: The center of curvature is not exactly on the optical axis!)

       - x^3                        3 x^2
  xc = -----             yc = 2 f + -----
       4 f^2                         4 f

  mit f = Brennweite  focal length
      x = Koordinate in radialer Richtung  coordinate in radial direction
 

Ein Strahl der senkrecht auf der Spiegeloberfläche steht schneidet die Y-Achse bei:
(Wichtig beim Foucault-Test mit bewegter Lichtquelle und beim Laser-Foucault-Test)
A ray which is perpendicular to the mirror surface crosses the Y axis at:
(This is important for the Foucault test with moving light source, and for the laser Foucault test)

              x^2
  ycc = 2 f + ---
              4 f

  mit f = Brennweite  focal length
      x = Koordinate in radialer Richtung  coordinate in radial direction
 

Beim Foucault-Test mit feststehender Lichtquelle gilt:
This is the formula for the Foucault test with non-moving light source:

            x^2    x^4 
ycc = 2 f + --- + ------   (Die Formel ist exakt und keine Näherung)
            2 f   16 f^3 

Dabei ist zu beachten dass diese Formeln nur dann gelten, wenn sich die unbewegliche Lichtquelle
genau im Krümmungsmittelpunkt der Spiegelmitte befindet.
Please note that these formulas are only valid if the non-moving light source is located exactly
at the paraxial center of curvature.
 

Die Differenz zwischen sphärischem Spiegel und Parabolspiegel
The difference between the sphere and the parabola

Allgemeiner Fall: 

Die Parabel hat die Form

    x^2
y = ---
    4 f

Wenn wir die radiale Koordinate x auf den Bereich [-1...1] normieren, dann gilt für die neue Koordinate r:

r = 2 x / D   oder   x = r D / 2

Wenn wir ausserdem das Öffnungsverhältnis N definieren:

N = f / D

dann ergibt sich die Parabel in dieser Form:

    r^2 D
y = -----
    16 N

Die Sphäre berührt die Parabel tangential bei einer beliebigen Zone.
In diesem Berührpunkt wird das Lot auf der Spiegeloberfläche gebildet. Dieses Lot schneidet die Y-Achse bei:

            r^2 D
ycc = 2 f + -----
            16 N

Damit ergibt sich der Krümmungsradius der Sphäre als die Hypothenuse eines rechtwinkligen Dreiecks:

      r^2 D^2
R^2 = ------- + 4 f^2
         4 

Mit D = f / N kann man die Gleichung umformen zu:

               (  r^2       )
R = 2 f * sqrt ( ------ + 1 )
               ( 16 N^2     )

Oder als Reihenentwicklung:

          D r^2    D r^4       D r^6       5 D r^8
R = 2 f + ----- - -------- + --------- - ----------- + ...
          16 N    1024 N^3   32768 N^5   4194304 N^7
 

Für den Sonderfall r = 0 ergibt sich:

R = 2 f
 

Für den Sonderfall r = 0.5 ergibt sich:

               (   1        )
R = 2 f * sqrt ( ------ + 1 ) 
               ( 64 N^2     )
 

Für den Sonderfall r = 0.707 ergibt sich:

               (   1        )
R = 2 f * sqrt ( ------ + 1 ) 
               ( 32 N^2     )
 

Für den Sonderfall r = 0.866 ergibt sich:

               (   3        )
R = 2 f * sqrt ( ------ + 1 )
               ( 64 N^2     )
 

Für den Sonderfall r = 1 ergibt sich:

               (   1        )
R = 2 f * sqrt ( ------ + 1 ) 
               ( 16 N^2     )
 
 

Fall 1:  Case 1:

  Die Sphäre und die Parabel berühren sich im Scheitelpunkt der Parabel, und
  beide Kurven haben an diesem Punkt den gleichen Krümmungsradius. In diesem Fall gilt:
  The sphere and the parabola touch in the middle of the mirror and both have the same
  radius of curvature at this point. In this case the relationship between R and f is:

  R = 2 f

  mit R = Krümmungsradius der Sphäre  radius of curvature of the sphere
      f = Brennweite der Parabel  focal length of the parabola

  Die Differenz zwischen Sphäre und Parabel in Reihendarstellung:
  The difference between the sphere and the parabola as a series:

       x^4     x^6      5 x^8     7 x^10    21 x^12
  e = ----- + ------ + ------- + ------- + --------- + ... 
      8 R^3   16 R^5   128 R^7   256 R^9   1024 R^11 

  oder  or

        x^4      x^6       5 x^8       7 x^10       21 x^12
  e = ------ + ------- + --------- + ---------- + ------------ + ... 
      64 f^3   512 f^5   16384 f^7   131072 f^9  2097152 f^11

  mit R = Krümmungsradius der Sphäre  radius of curvature of the sphere
      f = Brennweite der Parabel  focal length of the parabola
      x = Koordinate in radialer Richtung  coordinate in radial direction

  Die grösste Abweichung tritt am Rand des Spiegels auf und ist näherungsweise:
  The biggest difference is at the edge of the mirror and is approximately:

            D^4         D^4
  e_max = -------  =  --------      <-- Dies sind Näherungen !  These are Approximations!
          128 R^3     1024 f^3

  mit D = Durchmesser des Spiegels  diameter of the mirror
      R = Krümmungsradius der Sphäre  radius of curvature of the sphere
      f = Brennweite der Parabel  focal length of the parabola
 

  Erste Ableitung:  First differential:

         x^3     3 x^5      5 x^7      35 x^9      63 x^11
  e' = ------ + ------- + -------- + --------- + ----------- + ... 
       16 f^3   256 f^5   2048 f^7   65536 f^9   524288 f^11 
 

  Zweite Ableitung:  Second differential:

         3 x^2    15 x^4    35 x^6     315 x^8     693 x^10
  e'' = ------ + ------- + -------- + --------- + ----------- + ...
        16 f^3   256 f^5   2048 f^7   65536 f^9   524288 f^11 
 
 

Fall 2: Case 2:

  Die Sphäre berührt die Parabel im Scheitelpunkt und am Rand des Spiegels.
  Die Abweichung zwischen beiden Kurven wird minimal.
  Die grösste Abweichung tritt bei der 70.7% Zone auf und ist nur ca. 1/4 so gross wie in Fall 1.
  In diesem Fall gilt nicht R = 2 f, sondern:
  The sphere touches the parabola in the middle and at the edge of the mirror.
  The difference between the two profiles becomes minimal.
  The biggest difference is at the 70.7% zone and is only 1/4 as big as in case 1.
  In this case the relationship R = 2 f is not valid, instead this formula must be used:

            D^2 
  R = 2 f + ---- 
            32 f

  oder nach f aufgelöst:  or:

      2 R + sqrt(4 R^2 - D^2) 
  f = -----------------------
                8

  mit R = Krümmungsradius der Sphäre  radius of curvature of the sphere 
      f = Brennweite der Parabel  focal length of the parabola
      D = Durchmesser des Spiegels  diameter of the mirror
 

  Die Differenz zwischen Sphäre und Parabel in Reihendarstellung:
  Man beachte das Minuszeichen vor dem ersten Term!
  The difference between the sphere and the parabola as a series:
  Please note the minus sign at the beginning! 

              x^2                         x^4
  e = - --------------- + ------------------------------------ + 
        256 f^3                              3 D^4     D^6 
        ------- + 16 f    64 f^3 + 3 f D^2 + ----- + -------- 
          D^2                                64 f    4096 f^3 

                                      x^6 
        ----------------------------------------------------------------- +
                               5 f D^4   5 D^6     5 D^8        D^10
        512 f^5 + 40 f^3 D^2 + ------- + ----- + --------- + -----------
                                  4      256 f   32768 f^3   2097152 f^5

                                                         5 x^8
        ------------------------------------------------------------------------------------------------------------ + ...
                    1792 f^6 D^2   84 f^5 D^4   35 f^4 D^6   35 f^3 D^8   21 f^2 D^10    7 f D^12         D^14
        16384 f^7 + ------------ + ---------- + ---------- + ---------- + ----------- + ----------- + -------------
                         f            f^2         16 f^3      1024 f^4     65536 f^5    4194304 f^6   268435456 f^7
 

  Die grösste Abweichung tritt bei der 70.7% Zone des Spiegels auf und ist näherungsweise:
  The biggest difference is at the 70.7% zone of the mirror and is approximately:

              D^4
  e_max = - --------      <-- Das ist eine Näherung ! This is an approximation!
            4096 f^3

  mit D = Durchmesser des Spiegels  diameter of the mirror
      f = Brennweite der Parabel  focal length of the parabola

  oder  or

               D
  e_max = - --------      <-- Das ist eine Näherung !  This is an approximation!
            4096 N^3

  mit N = f / D   (Öffnungsverhältnis)  (focal ratio)
 

  Die erste Ableitung der Differenz zwischen Sphäre und Parabel in Reihendarstellung:
  Man beachte das Minuszeichen vor dem ersten Term!
  The first differential of the difference between the sphere and the parabola as a series:
  Please note the minus sign at the beginning! 

               x                        4 x^3
  e' = - -------------- + ------------------------------------ +
         128 f^3                             3 D^4     D^6 
         ------- + 8 f    64 f^3 + 3 f D^2 + ----- + -------- 
           D^2                               64 f    4096 f^3

                                    6 x^5 
       ----------------------------------------------------------------- +
                              5 f D^4   5 D^6     5 D^8        D^10
       512 f^5 + 40 f^3 D^2 + ------- + ----- + --------- + -----------
                                 4      256 f   32768 f^3   2097152 f^5

                                                       40 x^7
       ------------------------------------------------------------------------------------------------------------ + ... 
                   1792 f^6 D^2   84 f^5 D^4   35 f^4 D^6   35 f^3 D^8   21 f^2 D^10    7 f D^12         D^14
       16384 f^7 + ------------ + ---------- + ---------- + ---------- + ----------- + ----------- + -------------
                        f            f^2         16 f^3      1024 f^4     65536 f^5    4194304 f^6   268435456 f^7
 

  Die zweite Ableitung der Differenz zwischen Sphäre und Parabel in Reihendarstellung:
  Man beachte das Minuszeichen vor dem ersten Term!
  The second differential of the difference between the sphere and the parabola as a series:
  Please note the minus sign at the beginning!

                1                       12 x^2
  e'' = - -------------- + ------------------------------------ +
          128 f^3                             3 D^4     D^6 
          ------- + 8 f    64 f^3 + 3 f D^2 + ----- + --------
            D^2                               64 f    4096 f^3 

                                    30 x^4
        ----------------------------------------------------------------- +
                               5 f D^4   5 D^6     5 D^8        D^10
        512 f^5 + 40 f^3 D^2 + ------- + ----- + --------- + -----------
                                  4      256 f   32768 f^3   2097152 f^5

                                                        280 x^6
        ------------------------------------------------------------------------------------------------------------ + ...
                    1792 f^6 D^2   84 f^5 D^4   35 f^4 D^6   35 f^3 D^8   21 f^2 D^10    7 f D^12         D^14
        16384 f^7 + ------------ + ---------- + ---------- + ---------- + ----------- + ----------- + -------------
                         f            f^2         16 f^3      1024 f^4     65536 f^5    4194304 f^6   268435456 f^7

  Nullstellen:  zero crossings:

  e'(0) = 0
  e'(0.3536 D) = 0  (Näherung) (Approximation)

  Maximum am Spiegelrand:  Maximum at the edge of the mirror:

  e'(0.5 D) = D^3 / (256 f^3)   (Näherung) (Approximation)

  Minimum bei der 40.8% Zone:  Minimum at the 40.8% zone:

  x = sqrt(1/24) D = 0.2041 D   (Näherung) (Approximation)

  e'(0.2041 D) = -3 D^3 / (512 sqrt(6) f^3) = - D^3 / (418.05 f^3)   (Näherung) (Approximation)

  --> Die beiden Extremwerte sind betragsmässig nicht gleich gross. Das bedeutet dass dies noch nicht der
      optimale Fall ist um die Streifen-Dichte bzw. Re-Tracing Fehler zu minimieren.
  The absolute values at the two extreme points are not equal. This means that this isn't the optimum
      case for minimizing the fringe density and re-tracing errors.
 

Fall 3:  Case 3:

  Die Sphäre berührt die Parabel tangential bei der 86.6% Zone.
  Die Streifen-Dichte des Interferogramms wird minimal.
  Die maximale Streifen-Dichte tritt bei der 50% Zone und am Rand auf.
  The sphere touches the parabola at the 86.6% zone.
  The fringe density in the interferogram becomes a minimum.
  The maximum fringe density is at the 50% zone and at the edge.
 

Das Lot auf der Spiegeloberfläche (an der 86.6% Zone) schneidet die Y-Achse bei:

            3 D^2
ycc = 2 f + ----- 
            64 f

oder

            3 D
ycc = 2 f + ---- 
            64 N

Und für den Krümmungsradius der Sphäre gilt:

               (   3        )
R = 2 f * sqrt ( ------ + 1 ) 
               ( 64 N^2     )

oder als Reihenentwicklung:

          3 D       9 D         27 D           405 D
R = 2 f + ---- - --------- + ----------- - -------------- + ...
          64 N   16384 N^3   2097152 N^5   1073741824 N^7

oder

          3 D^2     9 D^4       27 D^6         405 D^8
R = 2 f + ----- - --------- + ----------- - -------------- + ...
          64 f    16384 f^3   2097152 f^5   1073741824 f^7
 
 
 

Der Kehrwert des Krümmungsradius der Sphäre:

1    1    (   3        ) -1/2
- = --- * ( ------ + 1 ) 
R   2 f   ( 64 N^2     )

oder als Reihenentwicklung:

1    1     3 D^2      9 D^4       15 D^6         105 D^8
- = --- - ------- + --------- - ----------- + --------------
R   2 f   256 f^3   65536 f^5   8388608 f^7   4294967296 f^9
 

Man beachte dass die Sphäre NICHT durch den Koordinatenursprung geht, denn die Sphäre schneidet die Y-Achse bei:

                  9 D         27 D           405 D
ys = ycc - R = --------- - ----------- + -------------- - ...
               16384 N^3   2097152 N^5   1073741824 N^7

oder

                 9 D^4       27 D^6         405 D^8
ys = ycc - R = --------- - ----------- + -------------- - ...
               16384 f^3   2097152 f^5   1073741824 f^7
 

In die Gleichung der Sphäre

         x^2    x^4     x^6      5 x^8 
y = ys + --- + ----- + ------ + ------- + ... 
         2 R   8 R^3   16 R^5   128 R^7

wird jetzt die Reihenentwicklung für 1/R eingesetzt:

         x^2   (  1     3 D^2      9 D^4       15 D^6         105 D^8           )
y = ys + --- * ( --- - ------- + --------- - ----------- + -------------- - ... )
          2    ( 2 f   256 f^3   65536 f^5   8388608 f^7   4294967296 f^9       )

         x^4   (  1     3 D^2      9 D^4       15 D^6         105 D^8           ) 3
       + --- * ( --- - ------- + --------- - ----------- + -------------- - ... )
          8    ( 2 f   256 f^3   65536 f^5   8388608 f^7   4294967296 f^9       )

         x^6   (  1     3 D^2      9 D^4       15 D^6         105 D^8           ) 5
       + --- * ( --- - ------- + --------- - ----------- + -------------- - ... )
         16    ( 2 f   256 f^3   65536 f^5   8388608 f^7   4294967296 f^9       )

         5 x^8   (  1     3 D^2      9 D^4       15 D^6         105 D^8           ) 7
       + ----- * ( --- - ------- + --------- - ----------- + -------------- - ... )   + ...
          128    ( 2 f   256 f^3   65536 f^5   8388608 f^7   4294967296 f^9       )
 

oder mit x = r * D/2:

         r^2 D^2   (  1     3 D^2      9 D^4       15 D^6         105 D^8           )
y = ys + ------- * ( --- - ------- + --------- - ----------- + -------------- - ... )
            8      ( 2 f   256 f^3   65536 f^5   8388608 f^7   4294967296 f^9       )

         r^4 D^4   (  1     3 D^2      9 D^4       15 D^6         105 D^8           ) 3
       + ------- * ( --- - ------- + --------- - ----------- + -------------- - ... )
           128     ( 2 f   256 f^3   65536 f^5   8388608 f^7   4294967296 f^9       )

         r^6 D^6   (  1     3 D^2      9 D^4       15 D^6         105 D^8           ) 5
       + ------- * ( --- - ------- + --------- - ----------- + -------------- - ... )
          1024     ( 2 f   256 f^3   65536 f^5   8388608 f^7   4294967296 f^9       )

         5 r^8 D^8   (  1     3 D^2      9 D^4       15 D^6         105 D^8           ) 7
       + --------- * ( --- - ------- + --------- - ----------- + -------------- - ... )   + ...
           32768     ( 2 f   256 f^3   65536 f^5   8388608 f^7   4294967296 f^9       )
 

Die Differenz zwischen Sphäre und Parabel:

         r^2 D^2   (    3 D^2      9 D^4       15 D^6         105 D^8           )
e = ys + ------- * ( - ------- + --------- - ----------- + -------------- - ... )
            8      (   256 f^3   65536 f^5   8388608 f^7   4294967296 f^9       )

         r^4 D^4   (  1     3 D^2      9 D^4       15 D^6         105 D^8           ) 3
       + ------- * ( --- - ------- + --------- - ----------- + -------------- - ... )
           128     ( 2 f   256 f^3   65536 f^5   8388608 f^7   4294967296 f^9      )

         r^6 D^6   (  1     3 D^2      9 D^4       15 D^6         105 D^8           ) 5
       + ------- * ( --- - ------- + --------- - ----------- + -------------- - ... )
          1024     ( 2 f   256 f^3   65536 f^5   8388608 f^7   4294967296 f^9       )

         5 r^8 D^8   (  1     3 D^2      9 D^4       15 D^6         105 D^8           ) 7
       + --------- * ( --- - ------- + --------- - ----------- + -------------- - ... )   + ...
           32768     ( 2 f   256 f^3   65536 f^5   8388608 f^7   4294967296 f^9       )
 

Die erste Ableitung der Differenz zwischen Sphäre und Parabel:

     r D^2   (    3 D^2      9 D^4       15 D^6         105 D^8           )
e' = ----- * ( - ------- + --------- - ----------- + -------------- - ... )
       4     (   256 f^3   65536 f^5   8388608 f^7   4294967296 f^9       )

       r^3 D^4   (  1     3 D^2      9 D^4       15 D^6         105 D^8           ) 3
     + ------- * ( --- - ------- + --------- - ----------- + -------------- - ... )
         32      ( 2 f   256 f^3   65536 f^5   8388608 f^7   4294967296 f^9       )

       3 r^5 D^6   (  1     3 D^2      9 D^4       15 D^6         105 D^8           ) 5
     + --------- * ( --- - ------- + --------- - ----------- + -------------- - ... )
          512      ( 2 f   256 f^3   65536 f^5   8388608 f^7   4294967296 f^9       )

       5 r^7 D^8   (  1     3 D^2      9 D^4       15 D^6         105 D^8           ) 7
     + --------- * ( --- - ------- + --------- - ----------- + -------------- - ... )   + ...
         4096      ( 2 f   256 f^3   65536 f^5   8388608 f^7   4294967296 f^9       )
 

  Die Kurve e'(x) ist von grosser Bedeutung für zwei Anwendungen:
  a) Sie bestimmt die Querabberation beim Foucault-Test
  b) Sie bestimmt die Re-Tracing Fehler beim Test mit dem Fizeau Interferometer
  Daher wird diese Kurve jetzt etwas genauer betrachtet:
  The curve e'(x) is important for two applications:
  a) For the transversal abberation in the Foucault test
  b) For the re-tracing errors in the Fizeau interferometer test
  Let's have a closer look at this curve:
 

Fall 4: Case 4:

  Die Sphäre berührt die Parabel tangential am Rand des Spiegels.
  The sphere touches the parabola at the edge of the mirror.

  Das Lot auf der Spiegeloberfläche (am Rand) schneidet die Y-Achse bei:

              D^2 
  ycc = 2 f + ---- 
              16 f
 
 

Fall 5: Case 5:

  Die Sphäre berührt die Parabel am Rand des Spiegels und hat an diesem Punkt den gleichen Krümmungsradius.
  Die grösste Abweichung tritt in der Mitte des Spiegels auf.
  In diesem Fall gilt nicht R = 2 f, sondern:
  The sphere touches the parabola at the edge of the mirror and has the same radius of curvature at this point.
  The biggest difference is in the middle of the mirror.
  In this case the relationship R = 2 f is not valid, instead this formula must be used:
 

  R = sqrt(4 f^2 + (D^2)/4)   = 2 f + sqrt( 8 f^2 - (2 f sqrt(4 f^2 / (D^2)/4)) + (D^2)/4 )

  oder nach f aufgelöst:  or:

      sqrt(4 R^2 - D^2)
  f = -----------------
             4

  mit R = Krümmungsradius der Sphäre  radius of curvature of the sphere 
      f = Brennweite der Parabel  focal length of the parabola
      D = Durchmesser des Spiegels  diameter of the mirror
 

  Wer Fehler findet möge mir das bitte sagen!
  If you find bugs, please let me know!
 

Bedeutung der Variablen:  Meaning of the variables:

r1 ist die radiale Variable im Bereich [0..1], 0 auf der optischen Achse, 1 am Spiegelrand
r1 is the radial variable in the range [0..1], 0 on the optical axis, 1 at the edge
r2 = r1^2
r3 = r1^3
r4 = ...

t1 ist die Winkel-Variable
t1 is the angular variable
t2 = 2 t1
t3 = 3 t1
t4 = ...

Wichtig: Die Definition des Winkels "t" ist nicht eindeutig festgelegt. In der Literatur wird der Winkel t überwiegend im Uhrzeigersinn definiert, wobei der Nullpunkt oben liegt, also t = arctan(x/y).
Bei den meisten Software-Programmen ist die Definition entgegen dem Uhrzeigersinn mit dem Nullpunkt rechts, also t = arctan(y/x). Wenn man von der falschen Winkel-Definition ausgeht dann ändert sich zwar nichts an den Absolutbeträgen der Koeffizienten, aber viele Koeffizienten sind vertauscht (sin <--> cos) und viele Vorzeichen sind falsch.
Important: There is a lot of confusion about the definition of the angle t. In most older literature t is defined clockwise, which means t = arctan(x/y) , but in most software programs t is defined counter-clockwise, which means t = arctan(y/x) . If you use the wrong definition, then the absolute values are still correct, but a lot of coefficients are exchanged (sin <--> cos) and a lot of signs become wrong.

Um die Verwirrung komplett zu machen: Bei den meisten Software-Programmen zeigt die positive Y-Achse zwar nach oben, aber es gibt auch Programme bei denen die positive Y-Achse nach unten zeigt.
To make the confusion complete: In most software programs the positive Y axis is pointing up, but in some programs it's pointing down. 

Die folgende Liste zeigt welche Definition von diversen Software-Programmen und Buchautoren verwendet wird:
The following list shows which definition is used by some software programs and book authors:

IntelliWave: normalerweise arctan(y/x), kann aber geändert werden in arctan(x/y)
  normally arctan(y/x), but can be changed to arctan(x/y)
Zygo MetroPro: arctan(y/x), positive Y-Achse nach oben   positive Y-axis up
FringeXP: arctan(y/x), positive Y-Achse oben   positive Y-axis up
OpenFringe: arctan(y/x), positive Y-Achse oben   positive Y-axis up
BEAM4 from Stellar Software: arctan(x/y)
Seidel von Raphael Bugiel: arctan(x/y), positive Y-Achse unten bzw. vorne in der 3D-Darstellung
Jim Wyant, ZernikePolynomialsForTheWeb: arctan(y/x), positive Y-Achse oben positive Y-axis up
Daniel Malacara, Optical Shop Testing: arctan(x/y)
Daniel J. Schroeder, Astronomical Optics Second Edition: arctan(y/x)
Max Born & Emil Wolf, Principles of Optics, Sixth Edition: arctan(x/y)

Die Definition arctan(x/y) hat einen kleinen Vorteil: Wenn man die durch den Teststand hervorgerufenen Fehler eines Spiegels untersucht, dann müssen alle Zernike-Terme die sin() enthalten Null sein wenn der Teststand links-rechts symmetrisch ist.
The definition arctan(x/y) has a small advantage: If you regard the mirror's errors caused by the test stand, all Zernike terms containing sin() must be zero if the test stand has a left-right symmetry.

Sehr wichtig: Wenn man Zernike-Koeffizienten aus unterschiedlichen Quellen miteinander vergleicht, dann muss man sicherstellen dass in beiden Fällen das gleiche Koordinatensystem verwendet wurde !
--> Winkel-Definition überprüfen, t=arctan(x/y) oder t=arctan(y/x)
--> Positive Y-Achse überprüfen, oben oder unten
--> Drehwinkel der Kamera prüfen
--> Prüfen ob das Kamera-Bild eventuell spiegelverkehrt ist

Very important: When comparing Zernike coefficients from different sources with each other, you must make sure that in both cases the same coorcinate system was used !
--> Check the angle definition, t=arctan(x/y) or t=arctan(y/x)
--> Check the positive Y axis, up or down
--> Check the turning angle of the camera
--> Check if the camera's image is mirror reversed

                                                              PV         PV/RMS 
z[  0] := 1;                     constant (or piston)         0          0
z[  1] := (1*r1)*cos(t1);        tilt                         2          4 
z[  2] := (1*r1)*sin(t1);        tilt                         2          4
z[  3] := (2*r2-1);              focus (or power)             2          3.467
z[  4] := (1*r2)*cos(t2);        astigmatism 3rd order        2          4.899 = 2*sqrt(6)
z[  5] := (1*r2)*sin(t2);        astigmatism 3rd order        2          4.899 = 2*sqrt(6)
z[  6] := (3*r3-2*r1)*cos(t1);   coma 3rd order               1.629      5.663
z[  7] := (3*r3-2*r1)*sin(t1);   coma 3rd order               1.629      5.663
z[  8] := (6*r4-6*r2+1);         spherical 3rd order          1.5        4.478
z[  9] := (1*r3)*cos(t3);                triangular 5th order            5.663
z[ 10] := (1*r3)*sin(t3);                triangular 5th order            5.663
z[ 11] := (4*r4-3*r2)*cos(t2);           astigmatism 5th order           6.337
z[ 12] := (4*r4-3*r2)*sin(t2);           astigmatism 5th order           6.337
z[ 13] := (10*r5-12*r3+3*r1)*cos(t1);    coma 5th order                  6.942
z[ 14] := (10*r5-12*r3+3*r1)*sin(t1);    coma 5th order                  6.942
z[ 15] := (20*r6-30*r4+12*r2-1);         spherical 5th order             5.304
z[ 16] := (1*r4)*cos(t4);                       quadratic 7th order 
z[ 17] := (1*r4)*sin(t4);                        quadratic 7th order 
z[ 18] := (5*r5-4*r3)*cos(t3);                   triangular 7th order 
z[ 19] := (5*r5-4*r3)*sin(t3);                   triangular 7th order
z[ 20] := (15*r6-20*r4+6*r2)*cos(t2);            astigmatism 7th order
z[ 21] := (15*r6-20*r4+6*r2)*sin(t2);            astigmatism 7th order
z[ 22] := (35*r7-60*r5+30*r3-4*r1)*cos(t1);      coma 7th order
z[ 23] := (35*r7-60*r5+30*r3-4*r1)*sin(t1);      coma 7th order
z[ 24] := (70*r8-140*r6+90*r4-20*r2+1);          spherical 7th order
z[ 25] := (1*r5)*cos(t5);                                5-fold 9th order 
z[ 26] := (1*r5)*sin(t5);                                5-fold 9th order
z[ 27] := (6*r6-5*r4)*cos(t4);                           quadratic 9th order
z[ 28] := (6*r6-5*r4)*sin(t4);                           quadratic 9th order 
z[ 29] := (21*r7-30*r5+10*r3)*cos(t3);                   triangular 9th order
z[ 30] := (21*r7-30*r5+10*r3)*sin(t3);                   triangular 9th order
z[ 31] := (56*r8-105*r6+60*r4-10*r2)*cos(t2);            astigmatism 9th order
z[ 32] := (56*r8-105*r6+60*r4-10*r2)*sin(t2);            astigmatism 9th order
z[ 33] := (126*r9-280*r7+210*r5-60*r3+5*r1)*cos(t1);     coma 9th order
z[ 34] := (126*r9-280*r7+210*r5-60*r3+5*r1)*sin(t1);     coma 9th order
z[ 35] := (252*r10-630*r8+560*r6-210*r4+30*r2-1);        spherical 9th order
z[ 36] := (1*r6)*cos(t6);
z[ 37] := (1*r6)*sin(t6);
z[ 38] := (7*r7-6*r5)*cos(t5);
z[ 39] := (7*r7-6*r5)*sin(t5);
z[ 40] := (28*r8-42*r6+15*r4)*cos(t4);
z[ 41] := (28*r8-42*r6+15*r4)*sin(t4);
z[ 42] := (84*r9-168*r7+105*r5-20*r3)*cos(t3);
z[ 43] := (84*r9-168*r7+105*r5-20*r3)*sin(t3);
z[ 44] := (210*r10-504*r8+420*r6-140*r4+15*r2)*cos(t2);
z[ 45] := (210*r10-504*r8+420*r6-140*r4+15*r2)*sin(t2);
z[ 46] := (462*r11-1260*r9+1260*r7-560*r5+105*r3-6*r1)*cos(t1);
z[ 47] := (462*r11-1260*r9+1260*r7-560*r5+105*r3-6*r1)*sin(t1);
z[ 48] := (924*r12-2772*r10+3150*r8-1680*r6+420*r4-42*r2+1);   spherical 11th order
z[ 49] := (1*r7)*cos(t7);
z[ 50] := (1*r7)*sin(t7);
z[ 51] := (8*r8-7*r6)*cos(t6);
z[ 52] := (8*r8-7*r6)*sin(t6);
z[ 53] := (36*r9-56*r7+21*r5)*cos(t5);
z[ 54] := (36*r9-56*r7+21*r5)*sin(t5);
z[ 55] := (120*r10-252*r8+168*r6-35*r4)*cos(t4);
z[ 56] := (120*r10-252*r8+168*r6-35*r4)*sin(t4);
z[ 57] := (330*r11-840*r9+756*r7-280*r5+35*r3)*cos(t3);
z[ 58] := (330*r11-840*r9+756*r7-280*r5+35*r3)*sin(t3);
z[ 59] := (792*r12-2310*r10+2520*r8-1260*r6+280*r4-21*r2)*cos(t2);
z[ 60] := (792*r12-2310*r10+2520*r8-1260*r6+280*r4-21*r2)*sin(t2);
z[ 61] := (1716*r13-5544*r11+6930*r9-4200*r7+1260*r5-168*r3+7*r1)*cos(t1);
z[ 62] := (1716*r13-5544*r11+6930*r9-4200*r7+1260*r5-168*r3+7*r1)*sin(t1);
z[ 63] := (3432*r14-12012*r12+16632*r10-11550*r8+4200*r6-756*r4+56*r2-1);   spherical 13th order
z[ 64] := (1*r8)*cos(t8);
z[ 65] := (1*r8)*sin(t8);
z[ 66] := (9*r9-8*r7)*cos(t7);
z[ 67] := (9*r9-8*r7)*sin(t7);
z[ 68] := (45*r10-72*r8+28*r6)*cos(t6);
z[ 69] := (45*r10-72*r8+28*r6)*sin(t6);
z[ 70] := (165*r11-360*r9+252*r7-56*r5)*cos(t5);
z[ 71] := (165*r11-360*r9+252*r7-56*r5)*sin(t5);
z[ 72] := (495*r12-1320*r10+1260*r8-504*r6+70*r4)*cos(t4);
z[ 73] := (495*r12-1320*r10+1260*r8-504*r6+70*r4)*sin(t4);
z[ 74] := (1287*r13-3960*r11+4620*r9-2520*r7+630*r5-56*r3)*cos(t3);
z[ 75] := (1287*r13-3960*r11+4620*r9-2520*r7+630*r5-56*r3)*sin(t3);
z[ 76] := (3003*r14-10296*r12+13860*r10-9240*r8+3150*r6-504*r4+28*r2)*cos(t2);
z[ 77] := (3003*r14-10296*r12+13860*r10-9240*r8+3150*r6-504*r4+28*r2)*sin(t2);
z[ 78] := (6435*r15-24024*r13+36036*r11-27720*r9+11550*r7-2520*r5+252*r3-8*r1)*cos(t1);
z[ 79] := (6435*r15-24024*r13+36036*r11-27720*r9+11550*r7-2520*r5+252*r3-8*r1)*sin(t1);
z[ 80] := (12870*r16-51480*r14+84084*r12-72072*r10+34650*r8-9240*r6+1260*r4-72*r2+1);  spherical 15th order
z[ 81] := (1*r9)*cos(t9);
z[ 82] := (1*r9)*sin(t9);
z[ 83] := (10*r10-9*r8)*cos(t8);
z[ 84] := (10*r10-9*r8)*sin(t8);
z[ 85] := (55*r11-90*r9+36*r7)*cos(t7);
z[ 86] := (55*r11-90*r9+36*r7)*sin(t7);
z[ 87] := (220*r12-495*r10+360*r8-84*r6)*cos(t6);
z[ 88] := (220*r12-495*r10+360*r8-84*r6)*sin(t6);
z[ 89] := (715*r13-1980*r11+1980*r9-840*r7+126*r5)*cos(t5);
z[ 90] := (715*r13-1980*r11+1980*r9-840*r7+126*r5)*sin(t5);
z[ 91] := (2002*r14-6435*r12+7920*r10-4620*r8+1260*r6-126*r4)*cos(t4);
z[ 92] := (2002*r14-6435*r12+7920*r10-4620*r8+1260*r6-126*r4)*sin(t4);
z[ 93] := (5005*r15-18018*r13+25740*r11-18480*r9+6930*r7-1260*r5+84*r3)*cos(t3);
z[ 94] := (5005*r15-18018*r13+25740*r11-18480*r9+6930*r7-1260*r5+84*r3)*sin(t3);
z[ 95] := (11440*r16-45045*r14+72072*r12-60060*r10+27720*r8-6930*r6+840*r4-36*r2)*cos(t2);
z[ 96] := (11440*r16-45045*r14+72072*r12-60060*r10+27720*r8-6930*r6+840*r4-36*r2)*sin(t2);
z[ 97] := (24310*r17-102960*r15+180180*r13-168168*r11+90090*r9-27720*r7+4620*r5-360*r3+9*r1)*cos(t1);
z[ 98] := (24310*r17-102960*r15+180180*r13-168168*r11+90090*r9-27720*r7+4620*r5-360*r3+9*r1)*sin(t1);
z[ 99] := (48620*r18-218790*r16+411840*r14-420420*r12+252252*r10-90090*r8+18480*r6-1980*r4+90*r2-1);
z[100] := (1*r10)*cos(t10);
z[101] := (1*r10)*sin(t10);
z[102] := (11*r11-10*r9)*cos(t9);
z[103] := (11*r11-10*r9)*sin(t9);
z[104] := (66*r12-110*r10+45*r8)*cos(t8);
z[105] := (66*r12-110*r10+45*r8)*sin(t8);
z[106] := (286*r13-660*r11+495*r9-120*r7)*cos(t7);
z[107] := (286*r13-660*r11+495*r9-120*r7)*sin(t7);
z[108] := (1001*r14-2860*r12+2970*r10-1320*r8+210*r6)*cos(t6);
z[109] := (1001*r14-2860*r12+2970*r10-1320*r8+210*r6)*sin(t6);
z[110] := (3003*r15-10010*r13+12870*r11-7920*r9+2310*r7-252*r5)*cos(t5);
z[111] := (3003*r15-10010*r13+12870*r11-7920*r9+2310*r7-252*r5)*sin(t5);
z[112] := (8008*r16-30030*r14+45045*r12-34320*r10+13860*r8-2772*r6+210*r4)*cos(t4);
z[113] := (8008*r16-30030*r14+45045*r12-34320*r10+13860*r8-2772*r6+210*r4)*sin(t4);
z[114] := (19448*r17-80080*r15+135135*r13-120120*r11+60060*r9-16632*r7+2310*r5-120*r3)*cos(t3);
z[115] := (19448*r17-80080*r15+135135*r13-120120*r11+60060*r9-16632*r7+2310*r5-120*r3)*sin(t3);
z[116] := (43758*r18-194480*r16+360360*r14-360360*r12+210210*r10-72072*r8+13860*r6-1320*r4+45*r2)*cos(t2);
z[117] := (43758*r18-194480*r16+360360*r14-360360*r12+210210*r10-72072*r8+13860*r6-1320*r4+45*r2)*sin(t2);
z[118] := (92378*r19-437580*r17+875160*r15-960960*r13+630630*r11-252252*r9+60060*r7-7920*r5+495*r3-10*r1)*cos(t1);
z[119] := (92378*r19-437580*r17+875160*r15-960960*r13+630630*r11-252252*r9+60060*r7-7920*r5+495*r3-10*r1)*sin(t1);
z[120] := (184756*r20-923780*r18+1969110*r16-2333760*r14+1681680*r12-756756*r10+210210*r8-34320*r6+2970*r4-110*r2+1);

Zur Berechnung der Koeffizienten:

K(n,m,s) = binom(n-s,s) * binom(n-2s,(n+m)/2 - s)

mit binom(n,0) = 1  und  binom(n,k+1) = binom(n,k) * (n-k) / (k+1)

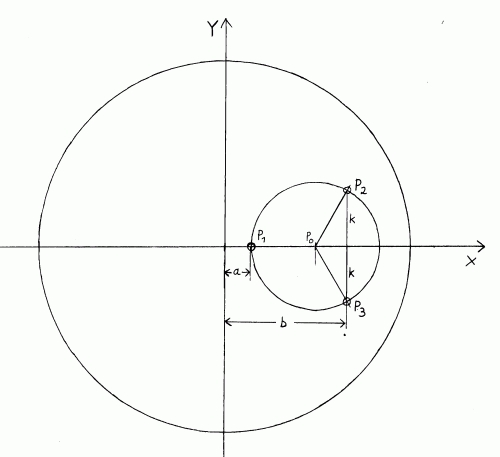
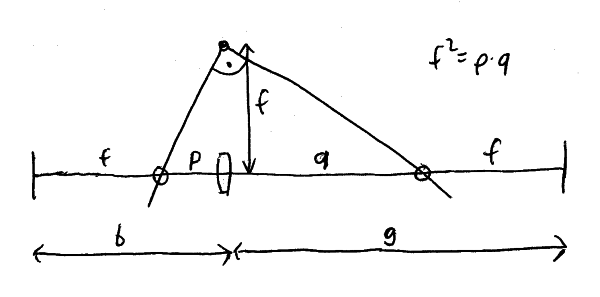
Dieses Bild zeigt einige graphische Darstellungen von Zernike-Polynomen. Je nachdem welche Definition für den Winkel verwendet wurde, entweder arctan(x/y) oder arctan(y/x), gilt eines der beiden Koordinatensysteme.
Das Bild wurde freundlicherweise von Alois Ortner zur Verfügung gestellt, es wurde mit dem Programm "Seidel" von Raphael Bugiel erstellt.
 
 

Symmetrien der Zernike-Polynome  Symmetries of Zernike polynomials

first yes/no answer is valid for angle definition t = arctan(x/y)
second yes/no answer is valid for angle definition t = arctan(y/x) 

Name:	Nr:	Polynomial:	Mirror Symmetry to X Axis	Mirror Symmetry to Y Axis	Rotational Symmetry 180 degrees	Rotational Symmetry 120 degrees
constant (or piston)	0	1	yes / yes	yes / yes	yes / yes	yes / yes
tilt	1	r * cos(t)	no  / yes	yes / no	no  / no	no  / no
tilt	2	r * sin(t)	yes / no	no  / yes	no  / no	no  / no
focus (or power)	3	2 * r^2 - 1	yes / yes	yes / yes	yes / yes	yes / yes
astigmatism 3rd order	4	r^2 * cos(2 * t)	yes / yes	yes / yes	yes / yes	no  / no
astigmatism 3rd order	5	r^2 * sin(2 * t)	no  / no	no / no	yes / yes	no  / no
coma 3rd order	6	(3 * r^3 - 2 * r) * cos(t)	no  / yes	yes / no	no  / no	no  / no
coma 3rd order	7	(3 * r^3 - 2 * r) * sin(t)	yes / no	no  / yes	no  / no	no  / no
spherical 3rd order	8	6 * r^4 - 6 * r^2 + 1	yes / yes	yes / yes	yes / yes	yes / yes
triangular 5th order	9	r^3 * cos(3 * t)	no  / yes	yes / no	no  / no	yes / yes
triangular 5th order	10	r^3 * sin(3 * t)	yes / no	no  / yes	no  / no	yes / yes
astigmatism 5th order	11	(4 * r^4 - 3 * r^2) * cos(2 * t)	yes / yes	yes / yes	yes / yes	no  / no
astigmatism 5th order	12	(4 * r^4 - 3 * r^2) * sin(2 * t)	no  / no	no  / no	yes / yes	no  / no
coma 5th order	13	(10 * r^5 - 12 * r^3 + 3 * r) * cos(t)	no  / yes	yes / no	no  / no	no  / no
coma 5th order	14	(10 * r^5 - 12 * r^3 + 3 * r) * sin(t)	yes / no	no  / yes	no  / no	no  / no
spherical 5th order	15	20 * r^6 - 30 * r^4 + 12 * r^2 - 1	yes / yes	yes / yes	yes / yes	yes / yes
quadratic 7th order	16	r^4 * cos(4 * t)	yes / yes	yes / yes	yes / yes	no  / no
quadratic 7th order	17	r^4 * sin(4 * t)	no  / no	no  / no	yes / yes	no  / no
triangular 7th order	18	(5 * r^5 - 4 * r^3) * cos(3 * t)	no  / yes	yes / no	no  / no	yes / yes
triangular 7th order	19	(5 * r^5 - 4 * r^3) * sin(3 * t)	yes / no	no  / yes	no  / no	yes / yes
astigmatism 7th order	20	(15 * r^6 - 20 * r^4 + 6 * r^2) * cos(2 * t)	yes / yes	yes / yes	yes / yes	no  / no
astigmatism 7th order	21	(15 * r^6 - 20 * r^4 + 6 * r^2) * sin(2 * t)	no / no	no  / no	yes / yes	no  / no
coma 7th order	22	(35 * r^7 - 60 * r^5 + 30 * r^3 - 4 * r) * cos(t)	no / yes	yes / no	no  / no	no / no
coma 7th order	23	(35 * r^7 - 60 * r^5 + 30 * r^3 - 4 * r) * sin(t)	yes / no	no  / yes	no  / no	no  / no
spherical 7th order	24	70 * r^8 - 140 * r^6 + 90 * r^4 - 20 * r^2 + 1	yes / yes	yes / yes	yes / yes	yes / yes

The rules for symmetries:
-- Polynomials that don't depend on angle t have all four symmetries
-- for definition t=arctan(x/y), all polynomials containing "cos" are mirror symmetrical to the Y axis
-- for definition t=arctan(x/y), all polynomials containing "cos(n * t)" are mirror symmetrical to the X axis if n = even
-- for definition t=arctan(x/y), all polynomials containing "sin(n * t)" are mirror symmetrical to the X axis if n = odd
-- for definition t=arctan(y/x), all polynomials containing "cos" are mirror symmetrical to the X axis
-- for definition t=arctan(y/x), all polynomials containing "cos(n * t)" are mirror symmetrical to the Y axis if n = even
-- for definition t=arctan(y/x), all polynomials containing "sin(n * t)" are mirror symmetrical to the Y axis if n = odd
-- Polynomials containing "sin(n * t)" or "cos(n * t)" have a 180 degrees rotational symmetry if n = even
-- Polynomials containing "sin(n * t)" or "cos(n * t)" have a 120 degrees rotational symmetry if n is a multiple of 3
 

Zernike-Polynome in x,y Koordinaten, und Ableitungen davon
Zernike Polynomials in x,y Coordinates, and Differentials of them

Achtung, nur gültig nur für die Winkel-Definition t = arctan(x/y)
 

Name	n	Polynom Z[n]	dZ[n]/dx	dZ[n]/dy
constant (or piston)	0	1	0	0
tilt	1	y	0	1
tilt	2	x	1	0
focus (or power)	3	2x2 + 2y2 - 1	4x	4y
astigmatism 3rd order	4	y2 - x2	-2x	2y
astigmatism 3rd order	5	2xy	2y	2x
coma 3rd order	6	3x2y + 3y3 - 2y	6xy	3x2 + 9y2 - 2
coma 3rd order	7	3x3 + 3xy2 - 2x	9x2 + 3y2 - 2	6xy
spherical 3rd order	8	6x4 + 12x2y2 + 6y4 - 6x2 - 6y2 + 1	24x3 + 24xy2 - 12x	24x2y + 24y3 - 12y
triangular 5th order	9	y3 - 3x2y	-6xy	3y2 - 3x2
triangular 5th order	10	3xy2 - x3	3y2 - 3x2	6xy
astigmatism 5th order	11	-3y2 + 3x2 + 4y4 - 4x4	6x - 16x3	-6y + 16y3
astigmatism 5th order	12	-6xy + 8y3x + 8x3y	-6y + 8y3 + 24x2y	-6x + 24y2x + 8x3
coma 5th order	13	3y - 12y3 - 12x2y + 10y5 + 20x2y3 + 10x4y	-24xy + 40xy3 + 40x3y	3 - 36y2 - 12x2 + 50y4 + 60x2y2 + 10x4
coma 5th order	14	3x - 12xy2 - 12x3 + 10xy4 + 20x3y2 + 10x5	3 - 12y2 - 36x2 + 10y4 + 60x2y2 + 50x4	24xy + 40xy3 + 40x3y5
spherical 5th order	15

Siehe auch:
Suiter, Star Tsting Astronomical Telescopes, Seite 160-166
H. Haferkorn, Bewertung optischer Systeme, Seite 242-251

-- Schwächung des Amplitudenbetrags in den Aussenbezirken der Austrittspupille verschlechtert das Auflösungsvermögen und verringert die ntensität in den Nebenmaxima (d.h. in den Beugungsringen)
-- Schwächung des Amplitudenbetrags im Zentrum der Austrittspupille verbessert das Auflösungsvermögen und erhöht die Intensität in den Nebenmaxima.
-- Die erzielbaren Effekte sind jedoch für die praktische Anwendung verhältnismässig gering.

Die ideale Transmissionsverteilung in der Austrittspupille ist eine Gauss´sche Glockenkurve:

T_(r) = exp(- r² / w²)

mit r = normierte radiale Variable im Bereich [0..1]
    w = Konstante, welche die Breite der Glockenkurve bestimmt

Da die Glockenkurve unendlich breit ist und die reale Apertur aber nur einen endlichen Durchmesser hat, muss die Glockenkurve am Rand "abgeschnitten" werden.

Die Transmission am Rand ist:

T₍₁₎ = exp(-1 / w²)

und daraus ergibt sich w:

w = sqrt( -1 / ln(T₍₁₎) )

Einige Beispiele:

T(1)	w
0.5	1.201
0.368	1.0
0.2	0.788
0.169	0.75
0.1	0.659
0.05	0.578
0.02	0.506
0.0183	0.5
0.01	0.466

Die Transmission T eines absorbierenden Filters hängt von der Schichtdicke s ab:

T_(s) = exp(-s * c)

wobei c eine materialabhängige Konstante ist

oder 

s = -ln(T) / c

Somit ergibt sich die Schichtdicke beim Apodisations-Fiter:

s_(r) = r² / (c * w²)

Es ist also eine einfache quadratische Abhängigkeit vom Radius.

Beim Bedampfen wird das Filter mit einem Motor gedreht, und vor dem Filter befindet sich eine Maske.
Diese Maske muss so beschaffen sein, dass abhängig vom Radius ein unterschiedlich langes Bogensegment bedampft wird. Die Länge dieses Bogensegments muss proportional zum Quadrat des Radius sein.
 

Die Formel zur Berechnung der kleinen Achse des Sekundärspiegels aus Texereau, "How to make a Telescope", Appendix G, ist nur eine Näherung. Dies sind die exakten Formeln:
The formula for the secondary's minor axis from Texereau, "How to make a telescope", Appendix G, is only an approximation.
Here are the exact formulas:

Hilfsgrössen: Auxiliary variables:
L = d (f-e) + t (D-d)
M = 2 (f-e) - (D-d)
N = 2 (f-e) + (D-d) 
a = L/M + L/N

mit with
D = Hauptspiegel-Durchmesser     Primary mirror diameter
d = Bildfeld-Durchmesser        Field diameter
f = Brennweite          Focal length
e = Pfeiltiefe = D^2 / (16 f)    Sagitta
t = Abstand vom Sekundärspiegel zur Bildebene   Distance from Secondary to focal plane

Offset = (L/M - L/N) / 2         Offset
Kleine_Achse = sqrt(a^2 - 4 Offset^2)  Secondary's minor axis
Große_Achse = sqrt(2) * a          Secondary's major axis

Man beachte dass der Sekundärspiegel um den Offset in Richtung zum Hauptspiegel hin verschoben wird, und zusätzlich um den Offset vom Okular weg verschoben wird. Wenn die Verschiebung in der Ebene des Sekundärspiegels gesucht ist, dann muss der Offset noch mit sqrt(2) multiplizert werden. 

Man beachte dass das Verhältnis von grosser zu kleiner Achse nicht exakt sqrt(2) ist! Für übliche Öffnungsverhältnisse ist die Abweichung von sqrt(2) aber vernachlässigbar klein.
Please note that the major/minor axis ratio is not exactly sqrt(2) !
 

Für beliebige Einfallswinkel gilt:

Kleine_Achse / Große_Achse = sqrt(1 - epsilon^2)

epsilon = sin(beta) / cos(alpha/2)
alpha = Öffnungswinkel des Lichtkegels
      = 2 arctan(D / 2f)
beta = Winkel zwischen der Kegelachse und der Normalen auf der Sekundärspiegel-Fläche
 

a) Kollimierung mit einer Filmdose

Eine transparente Kleinbild-Filmdose wird in den Okularauszun gesteckt. Der Boden der Filmdose wurde entfernt, und im Deckel befindet sich genau zentrisch ein Loch von ca. 4-5mm Durchmesser.
Wenn man durch dieses Loch schaut, dann sieht man zwei Dinge:
1. Die Mittenmarkierung des Hauptspiegels in einer Entfernung von f (entspricht der Brennweite des Hauptspiegels)
2. Man sieht das Loch durch das man schaut, weil es sich im Hauptspiegel spiegelt. Der Lichtweg vom Auge zum Loch hat zwar die Länge 2f, aber bedingt durch den Vergrösserungseffekt des Hauptspiegel scheint das Loch nur in einer Entfernung von f zu stehen.
Weil beide Objekte scheinbar in der gleichen Entfernung stehen, kann das Auge beide Objekte gleichzeitig scharf sehen.

Wenn die optische Achse um den Abstand x aussermittig im Okularauszug liegt, dann sieht man die beiden Objekte um 2x gegeneinander verschoben. Bei 1m Brennweite traue ich mir zu die beiden Objekte auf +-1mm genau gegeneinander zu zentrieren. Dann liegt die optische Achse maximal +-0.5mm aussermittig im Okularauszug.

Betrachten wir nun einige Fehlermöglichkeiten:

1. Was passiert, wenn sich das Loch 1mm aussermittig im Okularauszug befindet? Dann liegt die optische Achse nach der Justierung 1mm aussermittig im Okularauszug. Die Mittigkeit des Loches kann aber einfach überprüft werden. 

2. Was passiert, wenn die Hauptspiegel-Markierung 1mm aussermittig aufgeklebt wurde? Das bewirkt dass die optische Achse nach der Justierung 0.5mm aussermittig im Okularauszug liegt. 
 
 

b) Kollimierung mit Laserpointer.

Ein Laserpointer wird in den Okularauszug gesteckt. Es ist eine unverzichtbare Voraussetzung, dass der Laserstrahl exakt die Mitte des Hauptspieges trifft. Wenn man das nicht beachtet, dann ist die ganze Justierung völlig nutzlos, weil es effektiv eine Dejustierung ist.
Der Hauptspiegel wird dann so justiert, dass der Laserstrahl in sich selbst zurück reflektiert wird.
Wenn die optische Achse des Hauptspiegels um den Abstand x aussermittig im Okularauszug liegt, dann trifft der Laserstrahl um den Abstand 2x seitlich versetzt auf das Gehäuse des Lasers. Problematisch ist es, wenn die Strahlaustritts-Öffnung des Lasers so gross ist, dass man den Auftreffpunkt des reflektierten Strahls gar nicht sehen kann.
Wenn man annimmt dass man den Auftreffpunkt des Strahls auf +-1mm genau einstellen kann, dann würde die optische Achse maximal +-0.5mm aussermittig im Okularauszug liegen.

Betrachten wir nun einige Fehlermöglichkeiten:

1. Was passiert, wenn der Laserstrahl nicht exakt die Mitte des Hauptspiegels trifft, sondern 1mm daneben auftrifft? Dann liegt der Auftreffpunkt des Laserstrahls im Okularauszug ebenfalls um 1mm daneben. Das bewirkt dass die optische Achse nach der Justierung 0.5mm aussermittig im Okularauszug liegt. Ich vermute dass sich hier der grösste Fehler einschleichen kann, wenn nicht genau darauf geachtet wird dass wirklich die Mitte des Hauptspiegels getroffen wird.

2. Was passiert, wenn der Laser zwar exakt die Mitte des Hauptspiegels trifft, aber wenn der Laser 1mm aussermittig im Okularauszug sitzt? Dann liegt der Auftreffpunkt des reflektierten Strahls sogar 2mm daneben. Das bewirkt dass die optsche Achse nach der Justierung 1mm aussermittig im Okularauszug liegt.

3. Was passiert, wenn die Hauptspiegel-Markierung 1mm aussermittig aufgeklebt wurde? Dieser Fall ist identisch mit Fall 1.
 

Zusammenfassung:

Die Filmdosen-Methode ist einfach, billig, schnell und genau. Sie ist sowohl tagsüber und auch nachts anwendbar.

Die Laser-Methode ist teurer, zeitaufwändiger, und bei gewissenhafter Anwendung lässt sich etwa die gleiche Genauigkeit erreichen. Tagsüber kann es schwierig sein, den Auftreffpunkt des Strahls auf dem Hauptsiegel zu sehen. Das ist aber eine unverzichtbare Voraussetzung für den Test. Im Vergleich zur Filmdosen-Methode gibt es mehr Fehlermögichkeiten.
 

Der grosse Kreis ist der parabolische Spiegel, von oben gesehen. Der kleine Kreis ist das Dreipunkt-Sphärometer mit dem Schwerpunkt P0 und den drei Auflagepunkten P1, P2 und P3. Genau genommen erscheint das Sphärometer von oben gesehen als Ellipse, da es leicht schräg im Raum liegt. Das Sphärometer wird entlang der x-Achse verschoben.  Eine Verdrehung des Sphärometers um seine eigene Achse wird ausgeschlossen, um die Berechnung nicht unnötig kompliziert zu machen. Die drei Auflagepunkte bilden ein gleichseitiges Dreieck, welches aber von oben gesehen perspektivisch verzerrt wird, da es leicht schräg im Raum liegt. k ist die Hälfte der Kantenlänge des Dreiecks. a und b sind die X-Koordinaten der Auflagepunkte.

Die Höhe des Paraboloids an einer beliebigen Stelle x,y wird durch diese Formel beschrieben:

z = (x^2 + y^2) / (4 f)

wobei f die Brennweite ist.

Der Auflagepunkt 1 hat die Koordinaten
x1 = a
y1 = 0
z1 = a^2 / (4 f)

Die Auflagepunkte 2 und 3 haben die Koordinaten
x2,3 = b
y2,3 = +-k
z2,3 = (b^2 + k^2) / (4 f)

wobei k die Hälfte der Kantenlänge des gleichseitigen Dreiecks ist.

Der folgende analytische Lösungsweg wurde von Ulrich Lange in de.sci.mathematik vorgeschlagen.

Als Parameter c wird der Neigungswinkel der Ebene, in der das Dreieck liegt, eingeführt. Da man aber gerne die Position des Sphärometers vorgeben möchte, muss der Neigungswinkel zuerst berechnet werden:

c = arctan(x / (2 f)) 

Das ist der Neigungswinkel, den das Paraboloid in der y=0 Ebene an der Stelle x hat. Diese Stelle stimmt näherungsweise mit dem Berührpunkt des Messtasters auf dem Paraboloid überein. Die Differenz ist in der Praxis vernachlässigbar.

Die Dreiecksebene lässt sich durch diese Gleichung beschreiben:

     a^2
z = ----- + (x - a) * tan(c)
    4 * f

Die Höhe des gleichseitigen Dreiecks ist h = sqrt(3) * k. Projiziert man die Höhe im Punkt 1 in die xy-Ebene, so erhält man für die x-Koordinate der Punkte 2 und 3:

b = a + sqrt(3) * k * cos(c)

Die Eckpunkte 2 und 3 sollen im Paraboloid z = (x^2 + y^2) / (4 f) und in der
Dreiecksebene z = a^2 + (x - a) * tan(c) liegen, also gilt:

b^2 + k^2    a^2 
--------- = ----- + (b - a) * tan(c)
  4 * f     4 * f

oder

b^2 + k^2 = a^2 + 4 * f * (b - a) * tan(c)

Einsetzen der Formel für b ergibt:

    4 * f * sqrt(3) * sin(c) - 3 * k * cos(c)^2 - k
a = -----------------------------------------------
             2 * sqrt(3) * cos(c)

Mit Hilfe der bereits oben angegebenen Gleichung kann nun b berechnet werden:

b = a + sqrt(3) * k * cos(c)

Die Koordinaten des Dreiecks-Schwerpunkts sind das arithmetische Mittel der Koordinaten der drei Eckpunkte:
x0 = (a + 2 * b) / 3
y0 = 0
z0 = (a^2 + 2 * (b^2 + k^2)) / (12 * f)

Der Messtaster liegt auf einer Geraden, die durch folgende Gleichung beschrieben wird:

         x0 - x
z = z0 + ------
         tan(c)

Gesucht ist nun der Berührpunkt des Messtasters auf dem Paraboloid. Dies ist der Schnittpunkt der Geraden mit der Parabel, die in der y=0 Ebene liegt:

     x^2
z = -----
    4 * f

Die Geradengleichung und die Parabelgleichung werden gleichgesetzt:

     x - x0    x^2 
z0 + ------ = -----
     tan(c)   4 * f

Das führt zu der quadratischen Gleichung

            f                  (  x0         )
x^2 + 4 * ------ * x - 4 * f * ( ------ + z0 ) = 0
          tan(c)               ( tan(c)      )

mit diesen zwei Lösungen für die x-Koordinate des Berührpunktes:

             (   -1          (    1           x0       z0  ))
xb = 2 * f * ( ------ +- sqrt( -------- + ---------- + --- )) 
             ( tan(c)        ( tan(c)^2   f * tan(c)    f  ))

Für c > 0 wird das negative und für c < 0 das positive Vorzeichen verwendet. Für c = 0 ist xb = 0.
Die z-Koordinate des Berührpunktes erhält man durch Einsetzen in die Parabelgleichung:

     xb^2
zb = -----
     4 * f

Der Messwert des Sphärometers ist die Strecke vom Dreiecks-Schwerpunkt zum Berührpunkt:

d = sqrt((x0 - xb)^2 + (z0 - zb)^2)

Es sei noch angemerkt, dass der Messtaster beim Parabolspiegel (im Gegensatz zum Kugelspiegel) nicht genau senkrecht zur Spiegel-Oberfläche steht.

Simulations-Programm für Sphärometer auf Paraboloid: Download

Simulations-Programm für unterschiedliche Sphärometer-Arten: Download
 

Die folgenden Angaben für die Genauigkeit eines Spiegels sind äquivalent:
-- Oberfläche +-1/16 lambda PV
-- Oberfläche 1/8 lambda PV
-- Wellenfront +- 1/8 lambda PV
-- Wellenfront 1/4 lambda PV

Bei Spiegeln mit annähernd senkrechtem Lichteinfall gilt generell: Der Wellenfront-Fehler ist doppelt so gross wie der Oberflächen-Fehler. Daher wird für Spiegel gerne der Oberflächen-Fehler angegeben, weil der Fehler dann kleiner ist und "besser" aussieht.

Mit "lambda" ist die Wellenlänge des Lichtes gemeint. Üblicherweise werden interferometrische Messungen mit einem roten Helium-Neon Laser bei 632.8nm gemacht. 

Raleigh-Kriterium: PV Wellenfront-Fehler < lambda/4

Bei Systemen mit mehreren Spiegeln ist zu beachten dass sich der gesamte Wellenfront-Fehler aus den Wellenfront-Fehlern der einzelnen Spiegel zusammensetzt. Im ungünstigsten Fall können sich alle Fehler addieren.
 
 

RMS:

RMS bedeutet "Root Mean Square", wörtlich übersetzt "Wurzel Mittel Quadrat", also der quadratische Mittelwert. Den PV Wert (Peak to Valley = höchste positive Spitze bis kleinste negative Spitze) kann man nicht direkt in einen RMS Wert umrechnen.
Bei einem Spiegel mit 1/4 lambda PV kann der RMS Wert theoretisch irgendwo zwischen fast Null und 1/8 lambda liegen. Es gibt keinen festen Umrechnungsfaktor zwischen PV und RMS. Der Faktor hängt von der Verteilung der Fehler auf der Fläche ab.

Für die Beurteilung der Qualität eines Spiegels ist in erster Linie der RMS Wert entscheidend.
 

Strehl-Zahl

Die Strehl-Zahl kann mit Näherungsformeln aus dem RMS-Wert des Wellenfrontfehlers (RMS_w) oder aus dem RMS-Wert des Oberflächenfehlers (RMS_s) berechnet werden:

SR = 1 - (2 Pi RMS_w)²     gültig für SR > 0.5
SR = 1 - (4 Pi RMS_s)²     gültig für SR > 0.5

SR = exp( -(2 Pi RMS_w)²)  gültig für SR > 0.1
SR = exp( -(4 Pi RMS_s)²)  gültig für SR > 0.1

mit
RMS_w = Quadratischer Mittelwert des Wellenfront-Fehlers, angegeben in Wellenlängen
RMS_s = Quadratischer Mittelwert des Oberflächen-Fehlers, angegeben in Wellenlängen

RMS_w = 2 * RMS_s

Total Integrated Scatter

TIS = (2 Pi RMS_w)²  = (4 Pi RMS_s)²

^{RMS_w = sqrt(TIS) / (2 * pi)}

^{RMS_s = sqrt(TIS) / (4 * pi)}
 

RMS_w	RMS_s	SR
0.2	0.1	0.206
0.15	0.075	0.390
0.12	0.06	0.566
0.1	0.05	0.674
0.08	0.04	0.777
0.06	0.03	0.868
0.05	0.025	0.907
0.04	0.02	0.939
0.03	0.015	0.965
0.02	0.01	0.984
0.015	0.0075	0.991
0.01	0.005	0.996

ISO 10110-5    Oberflächen-Fehler
ISO 10110-14   Wellenfront-Fehler

The following descriptions for a the accuracy of a mirror are equivalent:
-- Surface +-1/16 wave PV
-- Surface 1/8 wave PV
-- Wavefront +- 1/8 wave PV
-- Wavefront 1/4 wave PV
 
 
 
 
 

Strehl Ratio

Approximations:

SR = 1 - (2 pi RMS_w)²     good for SR > 0.5

SR = exp( -(2 pi RMS_w)²)   good for SR > 0.1

with
  RMS_w = root mean square of wavefront error in wavelengths
 

Die Form eines Kegelschnitts wird so definiert:
The shape of a conic section is defined by this formula:

                     x^2
  y = ------------------------------------ 
      R (1 + sqrt(1 - (x^2/R^2) (SC + 1)))

  mit R = paraxialer Krümmungsradius  paraxial radius of curvature
      x = Koordinate in radialer Richtung  coordinate in radial direction
      SC = Schwarzschild-Konstante, wird auch als "konische Konstante" oder "asphärische Konstante" bezeichnet
  Schwarzschild constant, also known as "conic constant" or "aspheric deformation constant"

Ein unterkorrigierter Parabolspiegel hat in der Mitte und am Rand einen Berg, und bei der 70% Zone ein Tal. Die Konische Konstante ist größer als -1 (zum Beispiel -0.95), somit handelt es sich um eine Ellipse.
Ein überkorrigierter Parabolspiegel hat in der Mitte und am Rand ein Tal, und bei der 70% Zone einen Berg. Die Konische Konstante ist kleiner als -1 (zum Beispiel -1.05), somit handelt es sich um eine Hyperbel.
 

Oberfläche Surface	Schwarzschild-Konstante SC oder konische Konstante CC oder asphärische Konstante Schwarzschild constant SC or conic constant CC or Aspheric Deformation Constant	Exzentrizität EX Excentricity EX	"SHAPE" Parameter, wird in der "BEAM3" Software verwendet SHAPE parameter, is used in "BEAM3" software "Aparabolic Deformation Constant"
Ellipse Oblate Ellipse	> 0	undefined	> 1
Kreis Circle	0	0	1
Ellipse Prolate Ellipse	-1 < SC < 0	0 < ex < 1	0 < SH < 1
Parabel Parabola	-1	1	0
Hyperbel Hyperbola	< -1	> 1	< 0

Die Beziehungen zwischen Schwarzschild-Konstante SC, Exzentrizität EX und SHAPE Parameter SH:
The relationship between Schwarzschild constant SC, excentricity EX and SHAPE parameter SH:

SC = - EX^2       EX = sqrt(-SC)

SH = SC + 1       SC = SH - 1
 

Abbildung von Objekten in endlicher Entfernung
Imaging Objects in finite Distance

       (s-2f)^2
SC = - --------
         s^2

mit s = Entfernung vom Spiegel zum Objekt  Distance from mirror to object
    f = Brennweite des Spiegels  Focal length

Sonderfälle: Special cases:
s = 2f        -->  SC = 0  spherical mirror
s = infinite  -->  SC = -1   parabolic mirror
 

Darstellung des allgemeinen Kegelschnitts als Reihe:
Expressing the conic section as a series:

ein schwieriges Problem ...   a difficult problem...

zunächst einmal wird substituiert:  first we do some substitutions:

    SC + 1 
A = ------      B = x^2     C = 1 / R
     R^2

und damit vereinfacht sich der Kegelschnitt zu:
and this simplifies the conic section to this formula:

           C * B
y = --------------------- 
    1 + sqrt(1 - (B * A))

Das führt zu der quadratischen Gleichung:
This leads to the quadratic equation:

y^2 - (2C/A) y + (C^2 B/A) = 0

mit der Lösung:
with this solution:

 y     1        (  1     B  )
--- = --- - sqrt( --- - --- )
 C     A        ( A^2    A  )

Die Gleichung wird mit A multipliziert:
We multiply the whole equation by A:

y A
--- = 1 - sqrt(1 - AB)
 C

Für den Ausdruck sqrt(1 - x) gibt es eine Potenzreihenentwicklung:
For sqrt(1 - x) there exists a series:

                   x    x^2   x^3   5 x^4
sqrt(1 - x) = 1 - --- - --- - --- - ----- - ...
                   2     8    16     128

somit ergibt sich:  so we get:

y A   AB    (AB)^2   (AB)^3   5 (AB)^4
--- = --- + ------ + ------ + -------- + ...
 C     2      8        16       128

oder or

 y     B    A B^2   A^2 B^3   5 A^3 B^4
--- = --- + ----- + ------- + --------- + ...
 C     2      8       16         128

Nun werden die Substitutionen rückgängig gemacht, so dass wir die
Potenzreihenentwicklung des Kegelschnitts erhalten:
Now lets cancel the substitutions:

     1    ( x^2   A x^4   A^2 x^6   5 A^3 x^8       )
y = --- * ( --- + ----- + ------- + --------- + ... )
     R    (  2      8       16         128          )

wobei immer noch gilt:   where A is still:

    SC + 1
A = ------ 
     R^2

Wenn A eingesetzt wir ergibt sich:   If we cancel the A substitution too, we get:

    x^2   (SC+1) x^4   (SC+1)^2 x^6   5 (SC+1)^3 x^8 
y = --- + ---------- + ------------ + -------------- + ...
    2 R     8 R^3        16 R^5          128 R^7

oder mit der Definition SH = SC + 1
or with the definition SH = SC + 1

    x^2   SH x^4   SH^2 x^6   5 SH^3 x^8 
y = --- + ------ + -------- + ---------- + ...
    2 R   8 R^3     16 R^5     128 R^7
 

Kontrolle: Für die Parabel gilt SC = -1 oder SH = 0, also A = 0, damit ergibt sich
Check: For the parabola SC = -1 or SH = 0, A = 0, so we get

y = x^2 / (2 R)

was völlig korrekt ist.
which is absolutely correct.
 
 

Die Differenz zwischen Sphäre und Kegelschnitt
The difference between the sphere and the conic section

Die Sphäre und der Kegelschnitt berühren sich auf der optischen Achse, und
beide Kurven haben an diesem Punkt den gleichen Krümmungsradius.
The sphere and the conic section touch on the optical axis and both have the same
radius of curvature at this point.

Die Differenz zwischen Sphäre und Kegelschnitt in Reihendarstellung:
The difference between the sphere and the conic section as a series:
 

      SC x^4   (SC^2 + 2 SC) x^6   5 (SC^3 + 3 SC^2 + 3 SC) x^8 
e = - ------ - ----------------- - ---------------------------- + ...
      8 R^3         16 R^5                   128 R^7 

oder mit der Definition SH = SC + 1
or with the definition SH = SC + 1

    (1-SH) x^4   (1-SH^2) x^6   5 (1-SH^3) x^8 
e = ---------- + ------------ + -------------- + ...
      8 R^3         16 R^5        128 R^7 
 

Wie sehen die Interferenz-Streifen aus, wenn man
den Kegelschnitt gegen eine Sphäre testet?

Betrachten wir der Einfachheit halber nur das erste Glied der Reihenentwicklung
der Differenz zwischen Kegelschnitt und Sphäre:

    SC x^4 
e = ------      (Näherung)
    8 R^3 

mit R = paraxialer Krümmungsradius  paraxial radius of curvature
    x = Koordinate in radialer Richtung  coordinate in radial direction
    SC = Schwarzschild-Konstante  Schwarzschild constant

Uns interessieren nun die Radien x, wo diese Differenz e gleich einem ganzzahligen Vielfachen
der halben Wellenlänge wird. Dies sind die Radien wo die hellen Interferenzstreifen liegen.
Natürlich nur unter der Annahme dass die beiden Kurven sich genau in der Mitte berühren, so
dass sich konzentrische Ringe um den Mittelpunkt bilden. In der Praxis dürfte es schwierig
sein diesen Justierzustand zu erreichen.

Für e soll also gelten: 

e = n lambda/2

mit n = ganze Zahl 0,1,2,3... welche die Nummer des Interferenzrings beschreibt
    lambda = Licht-Wellenlänge, beispielsweise 632.8nm

Die Gleichung 

SC x^4   n lambda
------ = --------      (Näherung)
8 R^3       2

hat die Lösung:

    ( 4 n lambda R^3 )
x = ( -------------- ) ^ (1/4)        (Näherung)
    (       SC       )

Oder in Worten: die vierte Wurzel aus dem was in der grossen Klammer steht.
Man sieht auch gleich dass es für SC=0 keine Lösung gibt, das ist der Sonderfall wenn
der Kegelschnitt eine Sphäre ist.
 
 

Die Differenz zwischen Parabel und Kegelschnitt
The difference between the parabola and the conic section

Die Parabel und der Kegelschnitt berühren sich auf der optischen Achse, und
beide Kurven haben an diesem Punkt den gleichen Krümmungsradius.
The parabola and the conic section touch on the optical axis and both have the same
radius of curvature at this point.

Die Differenz zwischen Parabel und Kegelschnitt in Reihendarstellung:
The difference between the parabola and the conic section as a series:

      (SC+1) x^4   (SC+1)^2 x^6   5 (SC+1)^3 x^8 
e = - ---------- - ------------ - -------------- - ...
        8 R^3        16 R^5          128 R^7 

oder mit der Definition SH = SC + 1
or with the definition SH = SC + 1

      SH x^4   SH^2 x^6   5 SH^3 x^8 
e = - ------ - -------- - ---------- - ...
      8 R^3     16 R^5     128 R^7 
 

  Für die Umrechnung in Zernike-Polynome muss x auf den Bereich [0..1] normiert werden,
  die neue Variable r ist 0 auf der optischen Achse und 1 am Rand des Spiegels:
  For the conversion into Zernike polynomials x must be normalized into the range [0..1],
  the new variable r is 0 on the optical axis and 1 at the edge of the mirror:

  r = 2 x / D       bzw.  x = r D / 2

  mit D = Durchmesser des Spiegels  diameter of the mirror
 

  Es ergibt sich diese Darstellung der Differenz zwischen Sphäre und Kegelschnitt:
  We get this formula for the difference between sphere and conic section:

        SH D^4        SH^2 D^6       5 SH^3 D^8 
  e = - ------- r^4 - -------- r^6 - ---------- r^8 - ...
        128 R^3       1024 R^5       32768 R^7 

  oder in kürzerer Schreibweise:
  or in a shorter written form:

  e = c4 r^4 + c6 r^6 + c8 r^8 + ...

  mit c4 = - SH D^4 / (128 R^3)
      c6 = - SH^2 D^6 / (1024 R^5) 
      c8 = -5 SH^3 D^8 / (32768 R^7)
 

  Offensichtlich sind hier nur die Winkel-unabhängigen Zernike-Polynome von Interesse:
  Obviously we need only the angle-independant Zernike polynomials in this case: